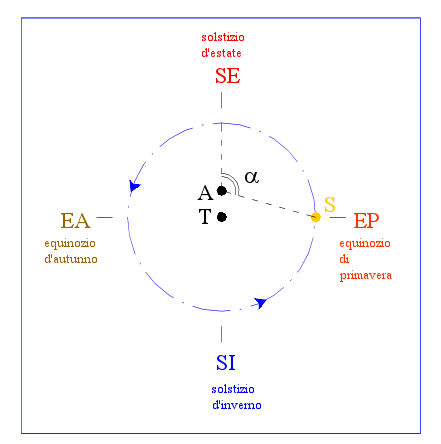
Il sistema geocentrico di Tolomeo (II sec. d. C.)

 

Il problema della creazione di una teoria planetaria che spiegasse i moti celesti, accompagnò il periodo ellenico ed ellenistico della storia dell'uomo con alcune sostanziali convinzioni (a parte alcune tesi eliocentriche tra le quali quelle di Eraclide Pontico e di Aristarco di Samo) che, dunque, fosse la Terra ad occupare il centro dell'universo, che la forma dello stesso fosse circolare, che anche le orbite dei pianeti fossero circolari e che anche le irregolarità riscontrate nei moti planetari dovessero spiegarsi, attraverso combinazioni geometriche opportune, di cerchi di varie dimensioni.

 

Tolomeo , vissuto approssimativamente ad Alessandria, tra il 100 ed il 170 d. C. dedica tutta la sua esistenza alla scienza astronomica e la sua fama è legata a quella del suo trattato: l' Almagesto .

In questa sua opera, muovendo dai risultati di Ipparco di Nicea (II sec. a. C.) ampiamente descritti ed elogiati, Tolomeo costruisce, elaborandola anche nei minuti dettagli, la grande macchina dell'universo geocentrico. Dei tredici libri di cui si compone l'Almagesto, i primi otto specialmente, sono basati sui risultati di Ipparco, mentre gli altri cinque sono dedicati alla teoria dei pianeti.

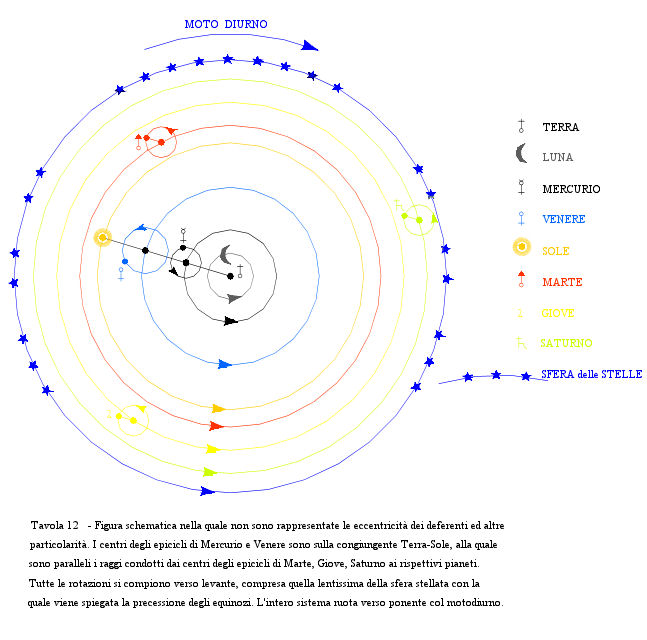
Secondo Tolomeo (vedi tavola 12) attorno alla Terra ruotavano le sfere dei sette pianeti posti così nell'ordine: Luna, Mercurio, Venere, Sole, Marte, Giove, Saturno . Tale disposizione rispettava la tradizione osservativa greca, che collocava più vicini, i pianeti dei quali si osservavano spostamenti più veloci, rispetto alle stelle dello Zodiaco e che quindi presentavano periodi di rivoluzione più brevi.

 

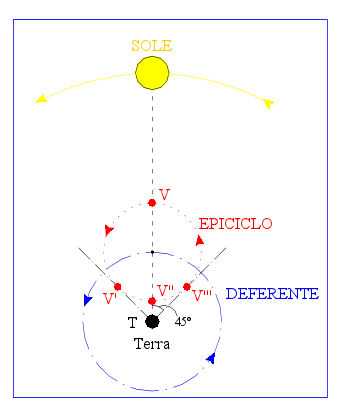
Figura 21: Sistema epiciclo-deferente

 

Un sistema epiciclo-deferente per Venere. Il deferente compie un giro all'anno, cosicchè se il centro dell'epiciclo si trova ad un certo istante allineato con la Terra e col centro del Sole rimarrà per sempre su questo allineamento e Venere non apparirà mai molto distante dal Sole. Gli angoli STV' e STV''' sono le angolazioni massime che si possono avere tra Sole e Venere e la condizione che queste siano di 45^0 determina completamente le misure relative dell'epiciclo e del deferente. V' è la posizione di massima distanza di Venere dal Sole quando assume gli aspetti mattutini e V''' è la simmetrica posizione rispetto a V' quando Venere assume gli aspetti serotini.

Per Mercurio e Venere, le cui rivoluzioni erano uguali al periodo di rivoluzione del Sole (un anno), Tolomeo accettò ancora dagli antichi l'opinione che i due pianeti si trovassero su orbite interne a quella del Sole. Gli sembrò verosimile distinguere i pianeti che potevano allontanarsi dal Sole di un qualsiasi angolo (pianeti con orbite esterne a quella del Sole), dai pianeti la cui distanza angolare dal Sole mai superava un certo limite.

Ogni pianeta, il Sole eccettuato, descriveva un epiciclo (cerchio minore) il cui centro percorreva un deferente (cerchio maggiore) (vedi figura 21) al fine di giustificare l'irregolarità del moto rispetto allo Zodiaco e le fasi di retrogradazione.

Il Sole si muoveva su un circolo eccentrico alla Terra (equante), per spiegare la maggiore velocità del moto dello stesso lungo l'eclittica dall'equinozio autunnale a quello primaverile, rispetto al moto dall'equinozio primaverile a quello autunnale (vedi figura 22).

Figura 22: L'equante

 

Il Sole si muove su un circolo che ha per centro la Terra (T) ma a velocità irregolare determinata dalla condizione che l'angolo a vari uniformemente col tempo.

Per spiegare la connessione delle posizioni di Mercurio e di Venere col Sole, i centri degli epicicli di questi due pianeti erano mantenuti sempre sulla congiungente Terra-Sole; pertanto i due pianeti non potevano essere osservati, dalla Terra, in una direzione formante con la congiungente un angolo superiore ad un certo valore, dipendente dal raggio del rispettivo epiciclo: maggiore, quindi, per Venere; minore per Mercurio.

Anche per gli altri pianeti si imponeva la necessità di creare un legame fra i loro movimenti ed il moto del Sole, al fine di spiegare perché il periodo epiciclico fosse connesso col periodo annuo, del quale, in realtà, era una riproduzione; a tale scopo i raggi degli epicicli di Marte, Giove e Saturno descrivevano, ciascuno, il proprio epiciclo in un anno, mantenendosi paralleli alla congiungente Terra-Sole. Ogni pianeta era condotto, dalla combinazione del moto del raggio del proprio epiciclo col moto dell'epiciclo sul deferente, a rioccupare la stessa posizione rispetto al Sole; ossia, ritornava in congiunzione od opposizione con questo, in un tempo eguale alla rivoluzione sinodica, mentre i raggi dei deferenti, compivano, ciascuno, una rotazione completa in una rivoluzione siderea.

In effetti, il modello adottato da Tolomeo prevedeva costruzioni geometriche ben più complesse, per dare ragione di irregolarità che, osservazioni più accurate, mettono in rilievo; irregolarità che derivavano dall'assunzione dogmatica della circolarità delle orbite.

Al di là delle sfere planetarie, Tolomeo, come già Aristotele (IV sec. a. C.), poneva la sfera delle stelle fisse o firmamento; ma, mentre per Aristotele il firmamento rappresentava anche il primo mobile, al quale era dovuta la rotazione diurna di tutto il sistema, per Tolomeo, firmamento e primo mobile erano separati. La necessità di separare l'ultima sfera, che produceva il moto diurno, dalla sfera delle stelle fisse, sorgeva dalla scoperta fatta da Ipparco, del fenomeno della precessione degli equinozi, che veniva spiegata con una rotazione di tutta la sfera stellata, da occidente ad oriente, intorno ai poli dell'eclittica. Essendo la sfera delle stelle fisse già dotata di questo movimento, il compito di produrre la rotazione diurna intorno ai poli del mondo, doveva essere assegnato ad un'altra sfera esterna; ed il primo mobile era, appunto, questa nona sfera che, con rapidissimo moto, trascinava tutte le sfere sottostanti.

Variazioni sul tempo | Chi siamo | Contattaci | webmaster Valentina Santopaolo