Il tempo e la relatività speciale

Valentina Santopaolo

Introduzione

La teoria della relatività speciale, formulata da Albert Einstein nel 1905, rappresenta non solo una importantissima rivoluzione scientifica, quanto una delle più importanti vittorie della mente umana sui concetti che, attraverso i secoli, erano divenuti veri ceppi della mente. Essa infatti analizza e distrugge il concetto di tempo assoluto ereditato dalla tradizione precedente e culminato nella trattazione newtoniana – l’immagine del tempo come qualcosa che scorre inesorabilmente in un flusso continuo – mostrandone la sua estraneità alla natura e il suo essere una costruzione linguistica. Il tempo nella cultura occidentale s’impone come flusso continuo, come categoria a priori della conoscenza: ma la storia della scienza dimostra che questa visione non è né quella più corretta né l’unica possibile. L’idea di tempo einsteiniana, come vedremo, è invero molto più simile alla concezione aristotelica.
Nell’antica Grecia ad esempio il tempo aveva forma circolare. Uno degli aspetti fondamentali della concezione antica del tempo è infatti l’esperienza ciclica: il “prima” e il “dopo”. Fu probabilmente l’osservazione della regolarità temporale del moto degli astri e della costanza dei ritmi biologici a conferire, per estensione, un’analoga struttura ciclica al tempo nel suo complesso.

Aristotele discute del Tempo Nel IV libro della Fisica. Secondo il filosofo il tempo è:

Questo, in realtà, è il tempo: il numero del movimento secondo il prima e il poi.
Aristotele, Fisica, IV, 11, 219b 1-2.

La numerazione del “prima” e del “poi” suppone l’anima (che è più corretto tradurre “mente”) come condizione indispensabile, perché soltanto l’intelligenza che è nell’anima ha la capacità di numerare. Pertanto, conclude Aristotele, è impossibile l’esistenza del tempo senza quella della mente.
Per Aristotele il tempo è ontologicamente secondario, giacché non esiste autonomamente, bensì come predicato del movimento. L’aspetto temporale del movimento, il suo poter essere contato, dal quale sorge il concetto di tempo, è invece del tutto reale.

 

Per capire  la teoria della relatività è utile fare alcune considerazioni preliminari.
Qualsiasi oggetto, ad esempio un treno fermo alla stazione, ha una posizione determinabile numericamente attraverso un sistema di coordinate cartesiane , e qualora viaggi,  poniamo a 100 Km all’ora, le sue posizioni sono sempre individuabili con un sistema di coordinate, in questo caso relativamente ai binari.
Poniamo ora che un passeggero del treno cammini in esso a 2 km all'ora. Tutte le sue posizioni sono anch’esse individuabili in un sistema di coordinate, naturalmente supponendo il treno, corpo di riferimento, immobile.

In generale possiamo affermare che se si vuole individuare un oggetto bisogna farlo rispetto a un corpo di riferimento e in un sistema di coordinate. E tutte le leggi della fisica hanno valore, per un determinato fenomeno, all'interno di un sistema di riferimento e in relazione a un preciso sistema di coordinate.
Il principio della relatività dei movimenti uniformi, suggerito da Galilei, mostra come, sulla base di osservazioni compiute all’interno di un determinato sistema, sia impossibile stabilire se tale sistema sia in quiete o in moto rettilineo uniforme, ciò equivale a dire che le leggi della fisica sono sempre della stessa forma nei sistemi di riferimento inerziali .

Ritorniamo al nostro passeggero. Il suo treno viaggia, come detto, a 100 Km all’ora, il passeggero stesso quindi percorrerà 100 km ogni ora. Supponiamo invece che egli cammini nella stessa direzione del treno ad una velocità di 2 Km all’ora.

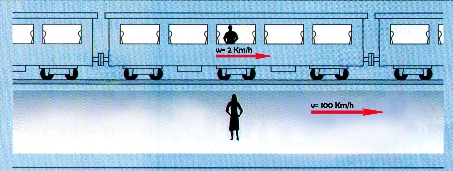
Per un osservatore fermo sui binari la sua velocità sarà 100+2 Km all’ora, ovvero, generalizzando:

W = v + w, dove W indica la velocità del viaggiatore rispetto all'osservatore a terra, v la velocità del treno e w la velocità del viaggiatore all'interno del treno.
Analogamente se il viaggiatore si muove in direzione apposta al treno otterremo:
W = v – w.

Queste semplici osservazioni però non sono verificate nel caso della propagazione della luce.
Infatti la teoria di Maxwell conclude nel definire una velocità della luce nell’etere di valore costante, chiamato c, uguale a 300.000 Km/s; altri studi, inoltre, stabiliscono che non esiste velocità superiore a quella della luce, per cui qualsiasi velocità, sommata a quella della luce, dà sempre una velocità uguale a quella della luce.
Riprendiamo come esempio la banchina ferroviaria (esempio citato dallo stesso Einstein) e immaginiamo che sia stata rimossa l’aria sopra di essa. Se si lancia un raggio di luce lungo la banchina, raggio che viaggia con velocità c rispetto ad essa, e supponendo che il treno viaggi con velocità v nella stessa direzione della luce, otterremo allora che la velocità della luce (c) rispetto al vagone è w=c-v. Per un vagone che viaggia con velocità uguale e opposta otterremo invece w=c+v.
Questo risultato, però, è in disaccordo con il principio di relatività. Infatti, secondo questo principio, la legge della costanza della velocità della luce nel vuoto dovrebbe avere la stessa validità, sia rispetto al treno in corsa, sia rispetto alla banchina; ma nell’esempio sopra citato la velocità di propagazione, rispetto alla banchina, risulta diversa da quella rispetto al treno in movimento. Si è dunque di fronte a una scelta: abbandonare il principio di relatività o abbandonare la legge della propagazione della luce nel vuoto.
A questo punto si profila la teoria della relatività.
Dall’analisi dei concetti di tempo e spazio, riferendoci ed essi come enti relativi al sistema di coordinate, e non assoluti, risultò che nella realtà non c’è contraddizione tra il principio di relatività e la legge di propagazione della luce e che usando entrambe le leggi si otteneva una teoria logicamente ineccepibile.
Questo è il nucleo di quella che Einstein stesso ha definito teoria della relatività speciale o ristretta.

 

Possiamo ora iniziare ad esaminare la teoria della relatività, affermando innanzitutto che essa è basata su due principi che possono essere così comparati:

Il primo principio è un’ipotesi empirica, sottoponibile alla verifica sperimentale, sicché, se risulta vera, descrive un fatto di natura.
Il secondo principio è invece una definizione, non v’è alcun modo di articolarlo come un fatto di natura, e non ha alcun senso chiedersi se sia vero o falso. Questo accade perché la velocità istantanea della luce è un concetto fisico privo di corrispondenza sperimentale; non v’è alcun modo di misurare la velocità della luce proprio a causa del suo valore massimo: la luce è l’agente più veloce del cosmo, e per calcolarla, avremmo bisogno di un fenomeno più veloce della luce stessa. Di conseguenza possiamo attribuire a questa grandezza fisica un valore arbitrario, senza paura che possa essere smentito dall’esperienza.
Einstein, adottando il secondo principio, sceglie di attribuire alla velocità istantanea della luce il valore c. Pur non essendoci alcun riscontro sperimentale e alcuna giustificazione logico-concettuale, il principio della costanza della velocità della luce trova la propria ragion d’essere nella sua utilità.
Così ancor prima di trattare la simultaneità e la sua qualità relativa, il fisico tedesco introduce una grandezza convenzionale, la definizione della velocità istantanea della luce. Questa convezione linguistica si rivela decisiva, come vedremo in seguito, per definire la natura relativa della simultaneità.

La trattazione di Einstein si divide in due parti: prima si stabilisce arbitrariamente cosa s’intenda per simultaneità tra due eventi non-locali; dopo si definisce, con l’aiuto delle leggi fisiche, un tempo relativo all’osservatore in moto uniforme. La relatività del tempo si fonda, appunto, sulla natura convenzionale del concetto di simultaneità a distanza.
Il punto di partenza del lavoro di Einstein è la divisione del tempo in due tempi epistemologicamente distinti: il tempo locale, cioè il tempo degli eventi che avvengono attorno a noi, e il tempo non-locale, cioè la datazione degli eventi lontani, dell’esistenza dei quali ci accorgiamo solo quando ne riceviamo notizia.
Si tratta quindi di distinguere tra simultaneità nello stesso luogo e simultaneità di eventi spazialmente separati; solo quest’ultima contiene il problema effettivo della simultaneità. La simultaneità nello stesso luogo, quindi il verificarsi di eventi nel medesimo posto e allo stesso tempo, viene chiamata “coincidenza”. Nel caso della coincidenza, quindi, non c’è alcun confronto di spazio e di tempo dal momento che essi sono identici per entrambi gli eventi. Pertanto il tempo locale non è l’oggetto della teoria della relatività, ma un suo presupposto epistemologico. La teoria infatti presuppone che esista l’orologio e che il suo funzionamento sia localmente perfetto.
Oggetto della teoria è esclusivamente il tempo a distanza, cioè il giudizio del “prima” e del “dopo” di eventi distanti; riguardo a ciò conclude che la relazione temporale è illusoria nel senso che il significato del “prima” e del “dopo” non è autoevidente, ma richiede una definizione semantica senza alcuna corrispondenza empirica.

 

Bisogna allora dimostrare la relatività del tempo; ciò è possibile dimostrando la relatività della simultaneità.
L’assioma sulla costanza della velocità della luce permette di stabilire in modo operativo quando due eventi sono simultanei.
Supponiamo che i fenomeni F1 e F2, collocati a grande distanza, consistano nell’emissione di luce da parte di due corpi che si trovano nei punti P1 e P2 dello spazio. Per un intervallo di tempo molto breve i due corpi diventano luminosi e la luce che essi emettono, propagandosi, permette a tutti gli osservatori di sapere che i due fenomeni hanno avuto luogo.

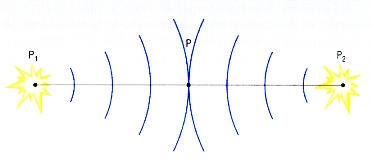
Diciamo che i fenomeni F1 e F2 (che avvengono nei punti P1 e P2) sono simultanei se la luce che essi emettono giunge nello stesso istante in un punto P equidistante da P1 e P2.
Proviamo ora ad applicare la definizione precedente a due casi concreti, in modo da analizzarne le conseguenze. Riprendendo un esempio inventato dallo stesso Einstein, consideriamo un treno che si muove a grande velocità rispetto a un osservatore 01 che si trova a terra, lungo i binari. Un secondo osservatore 02 si trova sul treno, esattamente nel punto medio del convoglio. A un certo punto, qualcuno provoca l’esplosione di due petardi sui binari, in corrispondenza delle due estremità del treno. Le due esplosioni sono testimoniate dai segni di bruciatura che rimangono sui binari e sul treno, e la luce emessa da esse si propaga in tutte le direzioni con velocità c.

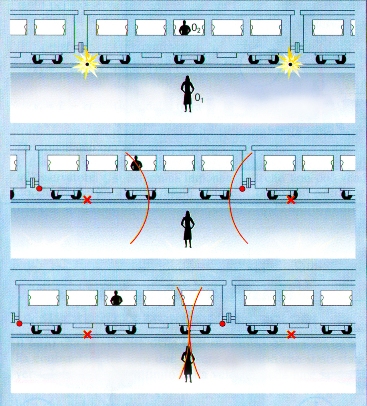
Supponiamo che i raggi luminosi emessi dai due petardi giungano a 01 nello stesso istante. Inoltre immaginiamo che l'osservatore 01, misurate le distanze tra il punto in cui si trovava quando ha visto le esplosioni e le due bruciature lasciate dalle esplosioni stesse, determini che tali distanze sono eguali. Sulla base della definizione precedente, egli è sicuro che i due petardi sono esplosi simultaneamente.
Secondo il senso comune, l'osservatore 02 deve essere senz'altro d'accordo con 01. E invece non è così: infatti, mentre i raggi luminosi si propagano, il treno si sposta (nel nostro esempio) verso sinistra. Quindi 02 vede prima l'esplosione che avviene alla testa del treno e soltanto dopo un certo intervallo di tempo l'esplosione che ha avuto luogo in coda al treno: non c'è dubbio che, secondo lui, le due esplosioni non sono state simultanee. Allora i due eventi che stiamo esaminando, cioè le due esplosioni, sono stati simultanee o no? Non c'è una risposta assoluta. Per quanto sembri strano l'unica risposta sensata è “dipende”. Infatti, entrambi gli osservatori si sono attenuti strettamente alla definizione operativa di simultaneità. Entrambi hanno condotto in modo corretto le loro osservazioni. Eppure le loro risposte sono diverse.
Va inoltre notato che non c'è nulla di speciale che distingua il sistema di riferimento del treno da quello in cui i binari sono fermi: in maniera del tutto simmetrica, due eventi che sono simultanei per l'osservatore 02 non lo sono per l'osservatore 01. Sulla base dell'invarianza della velocità della luce, dobbiamo quindi ammettere che il giudizio di simultaneità è relativo: due eventi che risultano simultanei in un dato sistema di riferimento non lo sono in un altro che si muove rispetto al primo.
Abbiamo quindi visto come un'analisi approfondita, svolta senza preconcetti, basata sul fatto che la velocità della luce ha un valore finito e indipendente dal sistema di riferimento, ci obbliga a concludere che il tempo assoluto su cui è fondata la meccanica classica non ha significato fisico; lo avrebbe soltanto se la luce si propagasse a velocità infinita. Soltanto in quel caso, il giudizio di simultaneità sarebbe assoluto, uguale per tutti gli osservatori.
Nella vita quotidiana, le velocità che riusciamo a ottenere sono così piccole rispetto alla velocità della luce che non è possibile avere un'esperienza diretta della relatività della simultaneità. Però l'analisi appena condotta non lascia dubbi. La simultaneità assoluta non esiste, non è possibile definire un tempo assoluto che “scorra” uguale per tutti gli osservatori; quel che ne deriva è il cosiddetto “rallentamento degli orologi”, fenomeno che possiamo concepire solo se ci riferimento al tempo come attributo proprio di un sistema di rifermento inerziale.

 

Ritornando all’esempio del treno e dell’osservatore a terra, Einstein mostra come il tempo che scorre nel vagone del treno visto da terra sia più lento del tempo che scorre a terra e viceversa.
Immaginiamo che sia il passeggero del treno che il capostazione abbiano un orologio ottico nel quale un fascio di luce si riflette contro uno specchio e torna indietro; nel momento in cui il treno passerà davanti il capostazione, esso vedrà l’orologio del passeggero descrivere non due linee rette come vede fare al suo orologio, bensì la traiettoria descritta dal fascio di luce dell’orologio del passeggero sarà una spezzata inclinata verso la direzione nella quale viaggia il treno. Ovviamente la situazione è invertibile, il passeggero osserverà lo stesso fenomeno nell’orologio del capostazione.

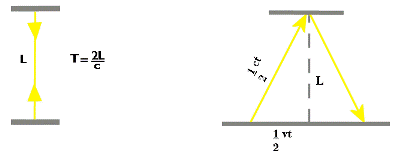
Orologio del capostazione               Orologio del passeggero del treno

Come noto la formula per calcolare il tempo è T=S/V dove S rappresenta lo spazio e V la velocità, mentre quella per calcolare lo spazio è S=VxT.
Dobbiamo dimostrare che il tempo che batte l’orologio del passeggero del treno è maggiore del tempo scandito dall’orologio del capostazione.
Nel caso dell’orologio del capostazione il tempo è dato dalla formula: T=2L/c (due volte la lunghezza del raggio di luce / la velocità della luce)

Nel caso dell’orologio del passeggero del treno applicando il teorema di Pitagora otteniamo:

(½ ct)2 =L2+ (½ vt)2 ;  ¼ c2 t2 = L2 + ¼ v2 t2  ;  ¼ c2 t2 - ¼ v2 t2 = L2; t2 ¼ (c2 - v2) = L2     

t2 =      4 L2   4          
c2 (1-v2/c2)

t =    2L/c   ® tempo del capostazione
√1- v2/c2

t =       T     4
√1- v2/c2  ® questo radicando è sempre minore di 1.

Vediamone le cause.
Il rapporto v2/c2 è fra la velocità del treno (v2) e quella della luce (c2); poiché è impossibile che il treno viaggi a velocità uguale o maggiore a quella della luce, il numeratore sarà sempre minore del denominatore, di conseguenza il risultato di questo rapporto sarà sempre minore di 1. Siamo giunti così al radicando √1- (un numero < 1); qualsiasi numero sottratto a 1 da sempre un numero < 1.
Quando v2=0 allora il radicando è 1. Di conseguenza il rapporto T/1 sarà uguale a T. Quindi il tempo del viaggiatore (t) e quello del capostazione (T) saranno equivalenti. È questo il caso del treno fermo in stazione.
Una delle conclusioni più inquietanti della teoria di Einstein è che gli orologi dei due osservatori, il viaggiatore e il capostazione, pur essendo del tutto identici non battono lo stesso tempo. Il tempo proprio di un fenomeno è quello misurato da un orologio solidale con il fenomeno, in questo caso l'orologio al polso del viaggiatore; ogni altro tempo sarà più lungo.
Il tempo, così come lo spazio, è un’esperienza immaginaria e non oggettiva. Esso è infatti, come scriveva Leibniz, è un ens rationis, un fenomeno mentale che nasce in conseguenza della successione delle cose, non affatto distante dalle affermazioni aristoteliche del IV secolo a.C.

Bibliografia essenziale